Note

Go to the end to download the full example code.

ASM3: dependency graph#

# Copyright (C) 2024 Juan Pablo Carbajal
# Copyright (C) 2024 Mariane Yvonne Schneider
#
# This program is free software; you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation; either version 3 of the License, or
# (at your option) any later version.
#
# This program is distributed in the hope that it will be useful,
# but WITHOUT ANY WARRANTY; without even the implied warranty of
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
# GNU General Public License for more details.
#
# You should have received a copy of the GNU General Public License
# along with this program. If not, see <http://www.gnu.org/licenses/>.

# Author: Juan Pablo Carbajal <ajuanpi@gmail.com>
import matplotlib.pyplot as plt
import numpy as np
from sympy import *
from pint import UnitRegistry

try:
    import dsafeatures
except ModuleNotFoundError:
    import sys
    import os

    sys.path.insert(0, os.path.abspath("../.."))

import dsafeatures.odemodel as m
import dsafeatures.symtools as st

from dsafeatures.printing import *
init_printing()

ureg = UnitRegistry()  # units registry

Load the model#

asm = m.ODEModel.from_csv(name="ASM3")
# States
X = asm.states
# Process rates
r_sym, r = asm.rates, asm.rates_expr
# Matrix
M = asm.coef_matrix
# State derivatives
dotX = asm.derivative(1)

Graph#

g = asm.graph

# nodes properties for visualization
vis_attr = {"isolated": dict(color="grey", size=1600),
            "rate": dict(color="gold", size=600),
            "measurement": dict(color="pink", size=1600),
            "state": dict(color="red", size=1600),
            "input": dict(color="violet", size=1600),
            "other": dict(color="black", size=800),
            }

# set initial positions
pos = st.nx.multipartite_layout(g, "layer")
p_ = np.asarray(list(pos.values()))
cnt = np.asarray([p_.max(axis=0)[0], p_.mean(axis=0)[1]])
# organize core
core = [n for n, d in g.nodes(data=True) if d["layer"] in ["rate", "state"]]
pos_core = st.nx.spring_layout(g.subgraph(core).to_undirected(), k=0.4, iterations=5000, center=cnt, seed=1234321)
pos.update(pos_core)
# orbit measurements and inputs
iso = [n for n, d in g.nodes(data=True) if d["layer"] in ["isolated", "other"]]
pos_meas = st.nx.spring_layout(g.to_undirected(), pos=pos, fixed=core+iso, k=0.5, iterations=1000)
pos.update(pos_meas)
# move isolated and other
mx = min(c[0] for c in pos.values())
for n in iso:
    pos[n][0] = mx

#N2, _ = asm.state_by_name("S_N2")
#pos[N2] -= pos[N2] * 0.4
#NE, _ = asm.state_by_name("X_UE")
#pos[NE] -= pos[NE] * 0.2
#Xh, _ = asm.state_by_name("X_OHO")
#pos[Xh] += [0.2, -0.15]
r_n = [n for n, d in g.nodes(data=True) if d["layer"]=="rate"]
pos[r_n[1]][1] += 0.25
st.nx.draw(g, pos=pos,
           node_color=[vis_attr[d["layer"]]["color"] for _, d in g.nodes(data=True)],
           node_size=[vis_attr[d["layer"]]["size"] for _, d in g.nodes(data=True)],
           with_labels=True,
           labels={x: latex(x, mode="inline") for x in g.nodes},
           arrowsize=20,
           )
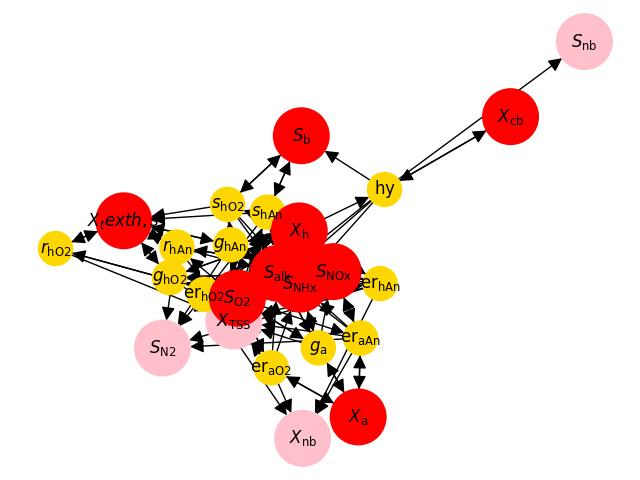
example asm3 graph

Model components#

Symbols and process rates name#

def to_latex(x):
    if "_" in x:
        p = x.split("_", 1)
        x = fr"{p[0]}_\text{{{p[1]}}}"
    return fr"${x}$"

for c in ("states", "processrates"):
    info_ = asm.component[c].rename(columns={"description": "Description"})
    info_["This work"] = info_.sympy.apply(lambda x: latex(x, mode='inline'))
    info_["Other name"] = info_.name.apply(to_latex)
    print(info_[["This work", "Other name", "Description"]].to_latex(index=False))

\begin{tabular}{lll}
\toprule
This work & Other name & Description \\
\midrule
$S_\text{b}$ & $S_\text{B}$ & Soluble biodegradable organics \\
$S_\text{nb}$ & $S_\text{U}$ & Soluble nondegradable organics \\
$S_\text{O2}$ & $S_\text{O2}$ & Dissolved oxygen \\
$X_\text{cb}$ & $XC_\text{B}$ & Particulate and colloidal biodegradable organics \\
$X_\text{nb}$ & $X_\text{U}$ & Particulate nonbiodegradable organics \\
$S_\text{NHx}$ & $S_\text{NHx}$ & Ammonia (NH4 + NH3) \\
$S_\text{NOx}$ & $S_\text{NOx}$ & Nitrate and nitrite (NO3 + NO2) (considered to be NO3 only for stoichiometry) \\
$S_\text{N2}$ & $S_\text{N2}$ & Dissolved nitrogen (gas, N2) \\
$X_\text{h}$ & $X_\text{OHO}$ & Ordinary heterotrophic organisms \\
$X_\text{a}$ & $X_\text{ANO}$ & Autotrophic nitrifying organisms (NH4+ to NO3-) \\
$X_text{h,s}$ & $X_\text{OHOStor}$ & Storage compound in ordinary heterotrophic organisms (OHOs) \\
$S_\text{alk}$ & $S_\text{Alk}$ & Alkalinity (HCO3-) \\
$X_\text{TSS}$ & $X_\text{TSS}$ & Total suspended solids \\
\bottomrule
\end{tabular}

\begin{tabular}{lll}
\toprule
This work & Other name & Description \\
\midrule
$\text{hy}$ & $hy$ & Hydrolysis \\
$s_\text{hO2}$ & $s_\text{hO2}$ & Aerobic storage of XOHO,Stor \\
$s_\text{hAn}$ & $s_\text{hAn}$ & Anoxic storage of XOHO,Stor \\
$g_\text{hO2}$ & $g_\text{hO2}$ & Aerobic growth of XOHO \\
$g_\text{hAn}$ & $g_\text{hAn}$ & Anoxic growth of XOHO (denitrification) \\
$\text{er}_\text{hO2}$ & $er_\text{hO2}$ & Aerobic endogenous respiration of XOHO \\
$\text{er}_\text{hAn}$ & $er_\text{hAn}$ & Anoxic endogenous respiration of XOHO \\
$r_\text{hO2}$ & $r_\text{hsO2}$ & Aerobic respiration of XOHO,Stor \\
$r_\text{hAn}$ & $r_\text{hsAn}$ & Anoxic respiration of XOHO,Stor \\
$g_\text{a}$ & $g_\text{a}$ & Growth of XANO (Nitrification) \\
$\text{er}_\text{aO2}$ & $er_\text{aO2}$ & Aerobic endogenous respiration of XANO \\
$\text{er}_\text{aAn}$ & $er_\text{aAn}$ & Anoxic endogenous respiration of XANO \\
\bottomrule
\end{tabular}

Description of active states

info_ = asm.component["states"].set_index("sympy")
info_ = [f"\item[{latex(x, mode='inline')}] {info_.loc[x].description}" for x in X if x in core]
info_ = [r"\begin{itemize}"] + info_ + [r"\end{itemize}"]
print("\n".join(info_))

/builds/sbrml/dsa-signal-features/doc/examples/example_asm3_graph.py:125: SyntaxWarning: invalid escape sequence '\i'
  info_ = [f"\item[{latex(x, mode='inline')}] {info_.loc[x].description}" for x in X if x in core]
\begin{itemize}
\item[$S_\text{O2}$] Dissolved oxygen
\item[$S_\text{b}$] Soluble biodegradable organics
\item[$S_\text{NHx}$] Ammonia (NH4 + NH3)
\item[$S_\text{NOx}$] Nitrate and nitrite (NO3 + NO2) (considered to be NO3 only for stoichiometry)
\item[$S_\text{alk}$] Alkalinity (HCO3-)
\item[$X_\text{cb}$] Particulate and colloidal biodegradable organics
\item[$X_\text{h}$] Ordinary heterotrophic organisms
\item[$X_text{h,s}$] Storage compound in ordinary heterotrophic organisms (OHOs)
\item[$X_\text{a}$] Autotrophic nitrifying organisms (NH4+ to NO3-)
\end{itemize}

Parameters#

info_ = asm.component["parameters"][["sympy", "value", "name", "unit", "description"]].copy()
info_.rename(columns={"description": "Description",
                      "value": "Value",
                      "unit": "Units"}, inplace=True)
info_["This work"] = info_.sympy.apply(lambda x: latex(x, mode='inline'))
info_["Other name"] = info_.name.apply(to_latex)
info_["Value"] = info_.Value.apply(lambda x: latex(x, mode='inline'))


def units_to_latex(x):
    try:
        y = ureg.parse_units(x)
        if y.dimensionless:
            # handle unit kinds, WIP in pint https://github.com/hgrecco/pint/pull/1967
            return x
        y = f"{y:Lx}"
        return y.replace("[","").replace("]","")
    except AssertionError:
        return "$-$"

info_["Units"] = info_.Units.apply(units_to_latex)
info_["Description"] = info_.Description.str.replace(r"\(([\\\w]+)[_]([\\\w]+)\)", r"($\1_\\text{\2}$)", regex=True)
info_.sort_values(by="This work", inplace=True)
print(info_[["This work", "Other name", "Value", "Units", "Description"]].to_latex(index=False))

\begin{tabular}{lllll}
\toprule
This work & Other name & Value & Units & Description \\
\midrule
$M_\text{N}$ & $M_\text{N}$ & $14.0$ & \si{\gram\per\mole} & atomic molar mass of nitrogen \\
$\eta_\text{an,h}$ & $n_\text{mOHOAx}$ & $0.6$ & $-$ & Reduction factor for anoxic growth of heterotrophs \\
$\gamma_\text{SBs,an}$ & $Y_\text{SBStorAx}$ & $0.8$ & g/g & Yield for XOHO,Stor formation per SB (Anoxic) \\
$\gamma_\text{SBsO2}$ & $Y_\text{SBStorOx}$ & $0.85$ & g/g & Yield for XOHO,Stor formation per SB (Aerobic ) \\
$\gamma_\text{a}$ & $Y_\text{ANO}$ & $0.24$ & g/g & Yield of autotrophs growth per SNO3 \\
$\gamma_\text{shO2}$ & $Y_\text{StorOHOOx}$ & $0.63$ & g/g & Yield for heterotrophs growth per XOHO,Stor (Aerobic ) \\
$\gamma_\text{shan}$ & $Y_\text{StorOHOAx}$ & $0.54$ & g/g & Yield for heterotrophs growth per XOHO,Stor (Anoxic) \\
$\iota_\text{COD,N2}$ & $i_\text{CODN2}$ & $\text{COD}_\text{N} / M_\text{N}$ & g/g & Conversion factor for N2 in COD \\
$\iota_\text{COD,NO3}$ & $i_\text{CODNO3}$ & $\left(\text{COD}_\text{N} + 3 \text{COD}_\text{O} + \text{COD}_{-}\right) / M_\text{N}$ & g/g & Conversion factor for NO3 in COD \\
$\iota_\text{NO3,N2}$ & $i_\text{NO3N2}$ & $\left(- 3 \text{COD}_\text{O} - \text{COD}_{-}\right) / M_\text{N}$ & g/g & Conversion factor for NO3 reduction to N2 \\
$\iota_\text{NSB}$ & $i_\text{NSB}$ & $0.03$ & g/g & N content of SB \\
$\iota_\text{NSnb}$ & $i_\text{NSU}$ & $0.01$ & g/g & N content of Snb \\
$\iota_\text{NXCB}$ & $i_\text{NXCB}$ & $0.04$ & g/g & N content of XB \\
$\iota_\text{NXb}$ & $i_\text{NXBio}$ & $0.07$ & g/g & N content of biomass (heterotrophs, XPAO, autotrophs) \\
$\iota_\text{NXnb}$ & $i_\text{NXU}$ & $0.02$ & g/g & N content of Xnb \\
$\iota_\text{TSS,XCB}$ & $i_\text{TSSXCB}$ & $0.75$ & g/g & Conversion factor XB in TSS \\
$\iota_\text{TSS,Xnb}$ & $i_\text{TSSXU}$ & $0.75$ & g/g & Conversion factor XU in TSS \\
$\iota_\text{TSS,Xs}$ & $i_\text{TSSXOHOStor}$ & $0.6$ & g/g & Conversion factor XSTO in TSS* \\
$\iota_\text{TSS_Xb}$ & $i_\text{TSSXBio}$ & $0.9$ & g/g & Conversion factor biomass in TSS \\
$\iota_\text{cSNHx}$ & $i_\text{ChargeSNHx}$ & $1 / M_\text{N}$ & \si{\mole\per\gram} & Conversion factor for NHx in charge \\
$\iota_\text{cSNOx}$ & $i_\text{ChargeSNOx}$ & $- 1 / M_\text{N}$ & \si{\mole\per\gram} & Conversion factor for NO3 in charge \\
$\kappa_\text{SB}$ & $K_\text{SBOHO}$ & $2.0$ & \si{\gram\per\meter\cubed} & Half-saturation coefficient for SB \\
$\kappa_\text{SNHxa}$ & $K_\text{NHxANO}$ & $1.0$ & \si{\gram\per\meter\cubed} & Half-saturation coefficient for SNHx \\
$\kappa_\text{SNHxh}$ & $K_\text{NHxOHO}$ & $0.01$ & \si{\gram\per\meter\cubed} & Half-saturation coefficient for SNHx \\
$\kappa_\text{SNOx}$ & $K_\text{NOxOHO}$ & $0.5$ & \si{\gram\per\meter\cubed} & Half-saturation coefficient for SNOx \\
$\kappa_\text{SO2a}$ & $K_\text{O2ANO}$ & $0.5$ & \si{\gram\per\meter\cubed} & Half-saturation coefficient for SO2 \\
$\kappa_\text{SO2h}$ & $K_\text{O2OHO}$ & $0.2$ & \si{\gram\per\meter\cubed} & Half-saturation coefficient for SO2 \\
$\kappa_\text{Salka}$ & $K_\text{AlkANO}$ & $0.5$ & \si{\mole\per\meter\cubed} & Half-saturation coefficient for SAlk \\
$\kappa_\text{Salkh}$ & $K_\text{AlkOHO}$ & $0.1$ & \si{\mole\per\meter\cubed} & Half-saturation coefficient for SAlk \\
$\kappa_\text{hyd,b}$ & $K_\text{XCBhyd}$ & $1.0$ & g/g & Half saturation parameter for XCB/XOHO \\
$\kappa_\text{sh}$ & $K_\text{StorOHO}$ & $1.0$ & g/g & Half-saturation coefficient for XOHO,Stor/XOHO \\
$\lambda_\text{hs}$ & $q_\text{SBStor}$ & $5.0$ & \si{\per\day} & Rate constant for XOHO,Stor storage \\
$\lambda_\text{hyd}$ & $q_\text{XCBSBhyd}$ & $3.0$ & g/g & Maximum specific hydrolysis rate \\
$\mu_\text{O2,a}$ & $m_\text{ANOOx}$ & $0.15$ & \si{\per\day} & Endogenous respiration rate for autotrophs (Aerobic) \\
$\mu_\text{O2e,h}$ & $m_\text{OHOOx}$ & $0.2$ & \si{\per\day} & Endogenous respiration rate of heterotrophs (Aerobic) \\
$\mu_\text{O2e,sh}$ & $m_\text{StorOx}$ & $0.2$ & \si{\per\day} & Endogenous respiration rate of XOHO,Stor (Aerobic) \\
$\mu_\text{an,a}$ & $m_\text{ANOAx}$ & $0.05$ & \si{\per\day} & Endogenous respiration rate for autotrophs (Anoxic) \\
$\mu_\text{ane,h}$ & $m_\text{OHOAx}$ & $0.1$ & \si{\per\day} & Endogenous respiration rate of heterotrophs (Anoxic) \\
$\mu_\text{ane,sh}$ & $m_\text{StorAx}$ & $0.1$ & \si{\per\day} & Endogenous respiration rate of XOHO,Stor (Anoxic) \\
$\mu_\text{a}$ & $m_\text{ANOMax}$ & $1.0$ & \si{\per\day} & Maximum growth rate of autotrophs \\
$\mu_\text{h}$ & $m_\text{OHOMax}$ & $2.0$ & \si{\per\day} & Maximum growth rate of heterotrophs \\
$\nu_\text{1,SNHx}$ & $v1_\text{SNHx}$ & $\iota_\text{NSB} \left(\zeta_\text{SUhy} - 1\right) - \iota_\text{NSnb} \zeta_\text{SUhy} + \iota_\text{NXCB}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{10,SNHx}$ & $v10_\text{SNHx}$ & $- \iota_\text{NXb} - 1 / \gamma_\text{a}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{10,SNOx}$ & $v10_\text{SNOx}$ & $1 / \gamma_\text{a}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{11,SNHx}$ & $v11_\text{SNHx}$ & $\iota_\text{NXb} - \iota_\text{NXnb} \zeta_\text{Xnb,l}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{12,SNHx}$ & $v12_\text{SNHx}$ & $\iota_\text{NXb} - \iota_\text{NXnb} \zeta_\text{Xnb,l}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{12,SNOx}$ & $v12_\text{SNOx}$ & $\frac{M_\text{N} \left(\zeta_\text{Xnb,l} - 1\right)}{- 3 \text{COD}_\text{O} - \text{COD}_{-}}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{2,SNHx}$ & $v2_\text{SNHx}$ & $\iota_\text{NSB}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{3,SNHx}$ & $v3_\text{SNHx}$ & $\iota_\text{NSB}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{3,SNOx}$ & $v3_\text{SNOx}$ & $\frac{M_\text{N} \left(\gamma_\text{SBs,an} - 1\right)}{- 3 \text{COD}_\text{O} - \text{COD}_{-}}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{4,SNHx}$ & $v4_\text{SNHx}$ & $- \iota_\text{NXb}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{5,SNHx}$ & $v5_\text{SNHx}$ & $- \iota_\text{NXb}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{5,SNOx}$ & $v5_\text{SNOx}$ & $\frac{M_\text{N} \left(\gamma_\text{shan} - 1\right)}{\gamma_\text{shan} \left(- 3 \text{COD}_\text{O} - \text{COD}_{-}\right)}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{6,SNHx}$ & $v6_\text{SNHx}$ & $\iota_\text{NXb} - \iota_\text{NXnb} \zeta_\text{Xnb,l}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{7,SNHx}$ & $v7_\text{SNHx}$ & $\iota_\text{NXb} - \iota_\text{NXnb} \zeta_\text{Xnb,l}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{7,SNOx}$ & $v7_\text{SNOx}$ & $\frac{M_\text{N} \left(\zeta_\text{Xnb,l} - 1\right)}{- 3 \text{COD}_\text{O} - \text{COD}_{-}}$ & g/g & stoichiometric correction factor for alkalinity \\
$\nu_\text{9,SNOx}$ & $v9_\text{SNOx}$ & $- \frac{M_\text{N}}{- 3 \text{COD}_\text{O} - \text{COD}_{-}}$ & g/g & stoichiometric correction factor for alkalinity \\
$\text{COD}_\text{C}$ & $COD_\text{C}$ & $32.0$ & \si{\gram\per\mole} & Theoretical COD of molar carbon \\
$\text{COD}_\text{Fe}$ & $COD_\text{Fe}$ & $24.0$ & \si{\gram\per\mole} & Theoretical COD of molar iron \\
$\text{COD}_\text{H}$ & $COD_\text{H}$ & $8.0$ & \si{\gram\per\mole} & Theoretical COD of molar hydrogen \\
$\text{COD}_\text{N}$ & $COD_\text{N}$ & $-24.0$ & \si{\gram\per\mole} & Theoretical COD of molar nitrogen \\
$\text{COD}_\text{O}$ & $COD_\text{O}$ & $-16.0$ & \si{\gram\per\mole} & Theoretical COD of molar oxygen \\
$\text{COD}_\text{P}$ & $COD_\text{P}$ & $40.0$ & \si{\gram\per\mole} & Theoretical COD of molar phosphorus \\
$\text{COD}_\text{S}$ & $COD_\text{S}$ & $48.0$ & \si{\gram\per\mole} & Theoretical COD of molar sulphur \\
$\text{COD}_{+}$ & $COD_\text{pos}$ & $-8.0$ & \si{\gram\per\mole} & Theoretical COD of positive charge \\
$\text{COD}_{-}$ & $COD_\text{neg}$ & $8.0$ & \si{\gram\per\mole} & Theoretical COD of negative charge \\
$\zeta_\text{SUhy}$ & $f_\text{SUXCBhyd}$ & $0.0$ & g/g & Fraction of inert COD generated in hydrolysis \\
$\zeta_\text{Xnb,l}$ & $f_\text{XUBiolys}$ & $0.2$ & g/g & Fraction of Xnb generated in biomass decay \\
\bottomrule
\end{tabular}

States vector#

print(latex(X))

\left[\begin{matrix}S_\text{O2}\\S_\text{b}\\S_\text{NHx}\\S_\text{NOx}\\S_\text{N2}\\S_\text{alk}\\S_\text{nb}\\X_\text{nb}\\X_\text{cb}\\X_\text{h}\\X_text{h,s}\\X_\text{a}\\X_\text{TSS}\end{matrix}\right]

Matrix#

M_entries = [Symbol(fr"m_{{{i}\,{j.name}}}") for i in X for j in r_sym]
Ms = Matrix(np.asarray(M_entries).reshape(*M.shape))
for i in range(M.shape[0]):
    for j in range(M.shape[1]):
        if isinstance(M[i, j], Number):
            Ms[i, j] = M[i, j]
print(latex(Ms))

\left[\begin{array}{cccccccccccc}0 & m_{S_\text{O2}\,s_\text{hO2}} & 0 & m_{S_\text{O2}\,g_\text{hO2}} & 0 & m_{S_\text{O2}\,\text{er}_\text{hO2}} & 0 & -1 & 0 & m_{S_\text{O2}\,g_\text{a}} & m_{S_\text{O2}\,\text{er}_\text{aO2}} & 0\\m_{S_\text{b}\,\text{hy}} & -1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\m_{S_\text{NHx}\,\text{hy}} & m_{S_\text{NHx}\,s_\text{hO2}} & m_{S_\text{NHx}\,s_\text{hAn}} & m_{S_\text{NHx}\,g_\text{hO2}} & m_{S_\text{NHx}\,g_\text{hAn}} & m_{S_\text{NHx}\,\text{er}_\text{hO2}} & m_{S_\text{NHx}\,\text{er}_\text{hAn}} & 0 & 0 & m_{S_\text{NHx}\,g_\text{a}} & m_{S_\text{NHx}\,\text{er}_\text{aO2}} & m_{S_\text{NHx}\,\text{er}_\text{aAn}}\\0 & 0 & m_{S_\text{NOx}\,s_\text{hAn}} & 0 & m_{S_\text{NOx}\,g_\text{hAn}} & 0 & m_{S_\text{NOx}\,\text{er}_\text{hAn}} & 0 & m_{S_\text{NOx}\,r_\text{hAn}} & m_{S_\text{NOx}\,g_\text{a}} & 0 & m_{S_\text{NOx}\,\text{er}_\text{aAn}}\\0 & 0 & m_{S_\text{N2}\,s_\text{hAn}} & 0 & m_{S_\text{N2}\,g_\text{hAn}} & 0 & m_{S_\text{N2}\,\text{er}_\text{hAn}} & 0 & m_{S_\text{N2}\,r_\text{hAn}} & 0 & 0 & m_{S_\text{N2}\,\text{er}_\text{aAn}}\\m_{S_\text{alk}\,\text{hy}} & m_{S_\text{alk}\,s_\text{hO2}} & m_{S_\text{alk}\,s_\text{hAn}} & m_{S_\text{alk}\,g_\text{hO2}} & m_{S_\text{alk}\,g_\text{hAn}} & m_{S_\text{alk}\,\text{er}_\text{hO2}} & m_{S_\text{alk}\,\text{er}_\text{hAn}} & 0 & m_{S_\text{alk}\,r_\text{hAn}} & m_{S_\text{alk}\,g_\text{a}} & m_{S_\text{alk}\,\text{er}_\text{aO2}} & m_{S_\text{alk}\,\text{er}_\text{aAn}}\\m_{S_\text{nb}\,\text{hy}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & m_{X_\text{nb}\,\text{er}_\text{hO2}} & m_{X_\text{nb}\,\text{er}_\text{hAn}} & 0 & 0 & 0 & m_{X_\text{nb}\,\text{er}_\text{aO2}} & m_{X_\text{nb}\,\text{er}_\text{aAn}}\\-1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 1 & -1 & -1 & 0 & 0 & 0 & 0 & 0\\0 & m_{X_text{h,s}\,s_\text{hO2}} & m_{X_text{h,s}\,s_\text{hAn}} & m_{X_text{h,s}\,g_\text{hO2}} & m_{X_text{h,s}\,g_\text{hAn}} & 0 & 0 & -1 & -1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 & -1\\m_{X_\text{TSS}\,\text{hy}} & m_{X_\text{TSS}\,s_\text{hO2}} & m_{X_\text{TSS}\,s_\text{hAn}} & m_{X_\text{TSS}\,g_\text{hO2}} & m_{X_\text{TSS}\,g_\text{hAn}} & m_{X_\text{TSS}\,\text{er}_\text{hO2}} & m_{X_\text{TSS}\,\text{er}_\text{hAn}} & m_{X_\text{TSS}\,r_\text{hO2}} & m_{X_\text{TSS}\,r_\text{hAn}} & m_{X_\text{TSS}\,g_\text{a}} & m_{X_\text{TSS}\,\text{er}_\text{aO2}} & m_{X_\text{TSS}\,\text{er}_\text{aAn}}\end{array}\right]

info_ = [fr"{latex(ms)} &\coloneqq {latex(m)} \\" for ms, m in zip(Ms, M) if not isinstance(m, Number)]
info_ = [r"\begin{align}"]+info_ + [r"\end{align}"]
print("\n".join(info_))

\begin{align}
m_{S_\text{O2}\,s_\text{hO2}} &\coloneqq \gamma_\text{SBsO2} - 1 \\
m_{S_\text{O2}\,g_\text{hO2}} &\coloneqq \frac{\gamma_\text{shO2} - 1}{\gamma_\text{shO2}} \\
m_{S_\text{O2}\,\text{er}_\text{hO2}} &\coloneqq \zeta_\text{Xnb,l} - 1 \\
m_{S_\text{O2}\,g_\text{a}} &\coloneqq \frac{\gamma_\text{a} + \iota_\text{COD,NO3}}{\gamma_\text{a}} \\
m_{S_\text{O2}\,\text{er}_\text{aO2}} &\coloneqq \zeta_\text{Xnb,l} - 1 \\
m_{S_\text{b}\,\text{hy}} &\coloneqq 1 - \zeta_\text{SUhy} \\
m_{S_\text{NHx}\,\text{hy}} &\coloneqq \iota_\text{NSB} \left(\zeta_\text{SUhy} - 1\right) - \iota_\text{NSnb} \zeta_\text{SUhy} + \iota_\text{NXCB} \\
m_{S_\text{NHx}\,s_\text{hO2}} &\coloneqq \iota_\text{NSB} \\
m_{S_\text{NHx}\,s_\text{hAn}} &\coloneqq \iota_\text{NSB} \\
m_{S_\text{NHx}\,g_\text{hO2}} &\coloneqq - \iota_\text{NXb} \\
m_{S_\text{NHx}\,g_\text{hAn}} &\coloneqq - \iota_\text{NXb} \\
m_{S_\text{NHx}\,\text{er}_\text{hO2}} &\coloneqq \iota_\text{NXb} - \iota_\text{NXnb} \zeta_\text{Xnb,l} \\
m_{S_\text{NHx}\,\text{er}_\text{hAn}} &\coloneqq \iota_\text{NXb} - \iota_\text{NXnb} \zeta_\text{Xnb,l} \\
m_{S_\text{NHx}\,g_\text{a}} &\coloneqq - \iota_\text{NXb} - \frac{1}{\gamma_\text{a}} \\
m_{S_\text{NHx}\,\text{er}_\text{aO2}} &\coloneqq \iota_\text{NXb} - \iota_\text{NXnb} \zeta_\text{Xnb,l} \\
m_{S_\text{NHx}\,\text{er}_\text{aAn}} &\coloneqq \iota_\text{NXb} - \iota_\text{NXnb} \zeta_\text{Xnb,l} \\
m_{S_\text{NOx}\,s_\text{hAn}} &\coloneqq \frac{\gamma_\text{SBs,an} - 1}{\iota_\text{NO3,N2}} \\
m_{S_\text{NOx}\,g_\text{hAn}} &\coloneqq \frac{\gamma_\text{shan} - 1}{\gamma_\text{shan} \iota_\text{NO3,N2}} \\
m_{S_\text{NOx}\,\text{er}_\text{hAn}} &\coloneqq \frac{\zeta_\text{Xnb,l} - 1}{\iota_\text{NO3,N2}} \\
m_{S_\text{NOx}\,r_\text{hAn}} &\coloneqq - \frac{1}{\iota_\text{NO3,N2}} \\
m_{S_\text{NOx}\,g_\text{a}} &\coloneqq \frac{1}{\gamma_\text{a}} \\
m_{S_\text{NOx}\,\text{er}_\text{aAn}} &\coloneqq \frac{\zeta_\text{Xnb,l} - 1}{\iota_\text{NO3,N2}} \\
m_{S_\text{N2}\,s_\text{hAn}} &\coloneqq \frac{1 - \gamma_\text{SBs,an}}{\iota_\text{NO3,N2}} \\
m_{S_\text{N2}\,g_\text{hAn}} &\coloneqq \frac{1 - \gamma_\text{shan}}{\gamma_\text{shan} \iota_\text{NO3,N2}} \\
m_{S_\text{N2}\,\text{er}_\text{hAn}} &\coloneqq \frac{1 - \zeta_\text{Xnb,l}}{\iota_\text{NO3,N2}} \\
m_{S_\text{N2}\,r_\text{hAn}} &\coloneqq \frac{1}{\iota_\text{NO3,N2}} \\
m_{S_\text{N2}\,\text{er}_\text{aAn}} &\coloneqq \frac{1 - \zeta_\text{Xnb,l}}{\iota_\text{NO3,N2}} \\
m_{S_\text{alk}\,\text{hy}} &\coloneqq \iota_\text{cSNHx} \nu_\text{1,SNHx} \\
m_{S_\text{alk}\,s_\text{hO2}} &\coloneqq \iota_\text{cSNHx} \nu_\text{2,SNHx} \\
m_{S_\text{alk}\,s_\text{hAn}} &\coloneqq \iota_\text{cSNHx} \nu_\text{3,SNHx} + \iota_\text{cSNOx} \nu_\text{3,SNOx} \\
m_{S_\text{alk}\,g_\text{hO2}} &\coloneqq \iota_\text{cSNHx} \nu_\text{4,SNHx} \\
m_{S_\text{alk}\,g_\text{hAn}} &\coloneqq \iota_\text{cSNHx} \nu_\text{5,SNHx} + \iota_\text{cSNOx} \nu_\text{5,SNOx} \\
m_{S_\text{alk}\,\text{er}_\text{hO2}} &\coloneqq \iota_\text{cSNHx} \nu_\text{6,SNHx} \\
m_{S_\text{alk}\,\text{er}_\text{hAn}} &\coloneqq \iota_\text{cSNHx} \nu_\text{7,SNHx} + \iota_\text{cSNOx} \nu_\text{7,SNOx} \\
m_{S_\text{alk}\,r_\text{hAn}} &\coloneqq \iota_\text{cSNOx} \nu_\text{9,SNOx} \\
m_{S_\text{alk}\,g_\text{a}} &\coloneqq \iota_\text{cSNHx} \nu_\text{10,SNHx} + \iota_\text{cSNOx} \nu_\text{10,SNOx} \\
m_{S_\text{alk}\,\text{er}_\text{aO2}} &\coloneqq \iota_\text{cSNHx} \nu_\text{11,SNHx} \\
m_{S_\text{alk}\,\text{er}_\text{aAn}} &\coloneqq \iota_\text{cSNHx} \nu_\text{12,SNHx} + \iota_\text{cSNOx} \nu_\text{12,SNOx} \\
m_{S_\text{nb}\,\text{hy}} &\coloneqq \zeta_\text{SUhy} \\
m_{X_\text{nb}\,\text{er}_\text{hO2}} &\coloneqq \zeta_\text{Xnb,l} \\
m_{X_\text{nb}\,\text{er}_\text{hAn}} &\coloneqq \zeta_\text{Xnb,l} \\
m_{X_\text{nb}\,\text{er}_\text{aO2}} &\coloneqq \zeta_\text{Xnb,l} \\
m_{X_\text{nb}\,\text{er}_\text{aAn}} &\coloneqq \zeta_\text{Xnb,l} \\
m_{X_text{h,s}\,s_\text{hO2}} &\coloneqq \gamma_\text{SBsO2} \\
m_{X_text{h,s}\,s_\text{hAn}} &\coloneqq \gamma_\text{SBs,an} \\
m_{X_text{h,s}\,g_\text{hO2}} &\coloneqq - \frac{1}{\gamma_\text{shO2}} \\
m_{X_text{h,s}\,g_\text{hAn}} &\coloneqq - \frac{1}{\gamma_\text{shan}} \\
m_{X_\text{TSS}\,\text{hy}} &\coloneqq - \iota_\text{TSS,XCB} \\
m_{X_\text{TSS}\,s_\text{hO2}} &\coloneqq \gamma_\text{SBsO2} \iota_\text{TSS,Xs} \\
m_{X_\text{TSS}\,s_\text{hAn}} &\coloneqq \gamma_\text{SBs,an} \iota_\text{TSS,Xs} \\
m_{X_\text{TSS}\,g_\text{hO2}} &\coloneqq \iota_\text{TSS_Xb} - \frac{\iota_\text{TSS,Xs}}{\gamma_\text{shO2}} \\
m_{X_\text{TSS}\,g_\text{hAn}} &\coloneqq \iota_\text{TSS_Xb} - \frac{\iota_\text{TSS,Xs}}{\gamma_\text{shan}} \\
m_{X_\text{TSS}\,\text{er}_\text{hO2}} &\coloneqq \iota_\text{TSS,Xnb} \zeta_\text{Xnb,l} - \iota_\text{TSS_Xb} \\
m_{X_\text{TSS}\,\text{er}_\text{hAn}} &\coloneqq \iota_\text{TSS,Xnb} \zeta_\text{Xnb,l} - \iota_\text{TSS_Xb} \\
m_{X_\text{TSS}\,r_\text{hO2}} &\coloneqq - \iota_\text{TSS,Xs} \\
m_{X_\text{TSS}\,r_\text{hAn}} &\coloneqq - \iota_\text{TSS,Xs} \\
m_{X_\text{TSS}\,g_\text{a}} &\coloneqq \iota_\text{TSS_Xb} \\
m_{X_\text{TSS}\,\text{er}_\text{aO2}} &\coloneqq \iota_\text{TSS,Xnb} \zeta_\text{Xnb,l} - \iota_\text{TSS_Xb} \\
m_{X_\text{TSS}\,\text{er}_\text{aAn}} &\coloneqq \iota_\text{TSS,Xnb} \zeta_\text{Xnb,l} - \iota_\text{TSS_Xb} \\
\end{align}

Rates vector#

print(latex(r_sym))

\left[\begin{matrix}\text{hy}{\left(X_\text{cb},X_\text{h} \right)}\\s_\text{hO2}{\left(S_\text{O2},S_\text{b},X_\text{h} \right)}\\s_\text{hAn}{\left(S_\text{NOx},S_\text{O2},S_\text{b},X_\text{h} \right)}\\g_\text{hO2}{\left(S_\text{NHx},S_\text{O2},S_\text{alk},X_\text{h},X_text{h,s} \right)}\\g_\text{hAn}{\left(S_\text{NHx},S_\text{NOx},S_\text{O2},S_\text{alk},X_\text{h},X_text{h,s} \right)}\\\text{er}_\text{hO2}{\left(S_\text{O2},X_\text{h} \right)}\\\text{er}_\text{hAn}{\left(S_\text{NOx},S_\text{O2},X_\text{h} \right)}\\r_\text{hO2}{\left(S_\text{O2},X_text{h,s} \right)}\\r_\text{hAn}{\left(S_\text{NOx},S_\text{O2},X_text{h,s} \right)}\\g_\text{a}{\left(S_\text{NHx},S_\text{O2},S_\text{alk},X_\text{a} \right)}\\\text{er}_\text{aO2}{\left(S_\text{O2},X_\text{a} \right)}\\\text{er}_\text{aAn}{\left(S_\text{NOx},S_\text{O2},X_\text{a} \right)}\end{matrix}\right]

info_ = [fr"{latex(r_)} &\coloneqq {latex(f_)} \\" for r_, f_ in zip(r_sym, r)]
info_ = [r"\begin{align}"]+info_ + [r"\end{align}"]
print("\n".join(info_))

\begin{align}
\text{hy}{\left(X_\text{cb},X_\text{h} \right)} &\coloneqq \frac{X_\text{cb} \lambda_\text{hyd}}{\frac{X_\text{cb}}{X_\text{h}} + \kappa_\text{hyd,b}} \\
s_\text{hO2}{\left(S_\text{O2},S_\text{b},X_\text{h} \right)} &\coloneqq \frac{S_\text{O2} S_\text{b} X_\text{h} \lambda_\text{hs}}{\left(S_\text{O2} + \kappa_\text{SO2h}\right) \left(S_\text{b} + \kappa_\text{SB}\right)} \\
s_\text{hAn}{\left(S_\text{NOx},S_\text{O2},S_\text{b},X_\text{h} \right)} &\coloneqq \frac{S_\text{NOx} S_\text{b} X_\text{h} \eta_\text{an,h} \kappa_\text{SO2h} \lambda_\text{hs}}{\left(S_\text{NOx} + \kappa_\text{SNOx}\right) \left(S_\text{O2} + \kappa_\text{SO2h}\right) \left(S_\text{b} + \kappa_\text{SB}\right)} \\
g_\text{hO2}{\left(S_\text{NHx},S_\text{O2},S_\text{alk},X_\text{h},X_text{h,s} \right)} &\coloneqq \frac{S_\text{NHx} S_\text{O2} S_\text{alk} X_text{h,s} \mu_\text{h}}{\left(S_\text{NHx} + \kappa_\text{SNHxh}\right) \left(S_\text{O2} + \kappa_\text{SO2h}\right) \left(S_\text{alk} + \kappa_\text{Salkh}\right) \left(\kappa_\text{sh} + \frac{X_text{h,s}}{X_\text{h}}\right)} \\
g_\text{hAn}{\left(S_\text{NHx},S_\text{NOx},S_\text{O2},S_\text{alk},X_\text{h},X_text{h,s} \right)} &\coloneqq \frac{S_\text{NHx} S_\text{NOx} S_\text{alk} X_text{h,s} \eta_\text{an,h} \kappa_\text{SO2h} \mu_\text{h}}{\left(S_\text{NHx} + \kappa_\text{SNHxh}\right) \left(S_\text{NOx} + \kappa_\text{SNOx}\right) \left(S_\text{O2} + \kappa_\text{SO2h}\right) \left(S_\text{alk} + \kappa_\text{Salkh}\right) \left(\kappa_\text{sh} + \frac{X_text{h,s}}{X_\text{h}}\right)} \\
\text{er}_\text{hO2}{\left(S_\text{O2},X_\text{h} \right)} &\coloneqq \frac{S_\text{O2} X_\text{h} \mu_\text{O2e,h}}{S_\text{O2} + \kappa_\text{SO2h}} \\
\text{er}_\text{hAn}{\left(S_\text{NOx},S_\text{O2},X_\text{h} \right)} &\coloneqq \frac{S_\text{NOx} X_\text{h} \kappa_\text{SO2h} \mu_\text{ane,h}}{\left(S_\text{NOx} + \kappa_\text{SNOx}\right) \left(S_\text{O2} + \kappa_\text{SO2h}\right)} \\
r_\text{hO2}{\left(S_\text{O2},X_text{h,s} \right)} &\coloneqq \frac{S_\text{O2} X_text{h,s} \mu_\text{O2e,sh}}{S_\text{O2} + \kappa_\text{SO2h}} \\
r_\text{hAn}{\left(S_\text{NOx},S_\text{O2},X_text{h,s} \right)} &\coloneqq \frac{S_\text{NOx} X_text{h,s} \kappa_\text{SO2h} \mu_\text{ane,sh}}{\left(S_\text{NOx} + \kappa_\text{SNOx}\right) \left(S_\text{O2} + \kappa_\text{SO2h}\right)} \\
g_\text{a}{\left(S_\text{NHx},S_\text{O2},S_\text{alk},X_\text{a} \right)} &\coloneqq \frac{S_\text{NHx} S_\text{O2} S_\text{alk} X_\text{a} \mu_\text{a}}{\left(S_\text{NHx} + \kappa_\text{SNHxa}\right) \left(S_\text{O2} + \kappa_\text{SO2a}\right) \left(S_\text{alk} + \kappa_\text{Salka}\right)} \\
\text{er}_\text{aO2}{\left(S_\text{O2},X_\text{a} \right)} &\coloneqq \frac{S_\text{O2} X_\text{a} \mu_\text{O2,a}}{S_\text{O2} + \kappa_\text{SO2a}} \\
\text{er}_\text{aAn}{\left(S_\text{NOx},S_\text{O2},X_\text{a} \right)} &\coloneqq \frac{S_\text{NOx} X_\text{a} \kappa_\text{SO2a} \mu_\text{an,a}}{\left(S_\text{NOx} + \kappa_\text{SNOx}\right) \left(S_\text{O2} + \kappa_\text{SO2a}\right)} \\
\end{align}

ODE#

def symb_to_dot(x):
    if "_" in x.name:
        p = x.name.split("_", 1)
        x = fr"\dot{{{p[0]}}}_{p[1]}"
    else:
        x = fr"\dot{{{x.name}}}"
    return x
dotX_sym = Matrix([Symbol(symb_to_dot(x)) for x in X])
dotX_expr = Ms * Matrix([Symbol(x_.name) for x_ in r_sym])
sub_order = ["state", "measurement", "isolated", "other"]
for layer in sub_order:
    info_ = []
    for x_, dx_, f_ in zip(X, dotX_sym, dotX_expr):
        if g.nodes[x_]["layer"] == layer:
            info_.append(fr"{latex(dx_)} &\coloneqq {latex(f_)} \\")
    if info_:
        info_ = [r"\begin{align}"]+ info_ + [fr"\label{{eq:asm1-ode-{layer}}}\end{{align}}"]
    print("\n".join(info_))

# info_ = []
# order = [0] * len(X)
# sub_order = ["state", "measurement", "isolated", "other"]
# for idx, x_dx_f_ in enumerate(zip(X, dotX_sym, dotX_expr)):
#     x_, dx_, f_ = x_dx_f_
#     order[idx] = sub_order.index(g.nodes[x_]["layer"])
#     info_.append(fr"{latex(dx_)} &\coloneqq {latex(f_)} \\")
# info_ = sorted(info_, key=lambda x_: order[info_.index(x_)])
# info_ = [r"\begin{align}"]+ info_ + [r"\end{align}"]
# print("\n".join(info_))

\begin{align}
\dot{S}_\text{O2} &\coloneqq \text{er}_\text{aO2} m_{S_\text{O2}\,\text{er}_\text{aO2}} + \text{er}_\text{hO2} m_{S_\text{O2}\,\text{er}_\text{hO2}} + g_\text{a} m_{S_\text{O2}\,g_\text{a}} + g_\text{hO2} m_{S_\text{O2}\,g_\text{hO2}} + m_{S_\text{O2}\,s_\text{hO2}} s_\text{hO2} - r_\text{hO2} \\
\dot{S}_\text{b} &\coloneqq \text{hy} m_{S_\text{b}\,\text{hy}} - s_\text{hAn} - s_\text{hO2} \\
\dot{S}_\text{NHx} &\coloneqq \text{er}_\text{aAn} m_{S_\text{NHx}\,\text{er}_\text{aAn}} + \text{er}_\text{aO2} m_{S_\text{NHx}\,\text{er}_\text{aO2}} + \text{er}_\text{hAn} m_{S_\text{NHx}\,\text{er}_\text{hAn}} + \text{er}_\text{hO2} m_{S_\text{NHx}\,\text{er}_\text{hO2}} + \text{hy} m_{S_\text{NHx}\,\text{hy}} + g_\text{a} m_{S_\text{NHx}\,g_\text{a}} + g_\text{hAn} m_{S_\text{NHx}\,g_\text{hAn}} + g_\text{hO2} m_{S_\text{NHx}\,g_\text{hO2}} + m_{S_\text{NHx}\,s_\text{hAn}} s_\text{hAn} + m_{S_\text{NHx}\,s_\text{hO2}} s_\text{hO2} \\
\dot{S}_\text{NOx} &\coloneqq \text{er}_\text{aAn} m_{S_\text{NOx}\,\text{er}_\text{aAn}} + \text{er}_\text{hAn} m_{S_\text{NOx}\,\text{er}_\text{hAn}} + g_\text{a} m_{S_\text{NOx}\,g_\text{a}} + g_\text{hAn} m_{S_\text{NOx}\,g_\text{hAn}} + m_{S_\text{NOx}\,r_\text{hAn}} r_\text{hAn} + m_{S_\text{NOx}\,s_\text{hAn}} s_\text{hAn} \\
\dot{S}_\text{alk} &\coloneqq \text{er}_\text{aAn} m_{S_\text{alk}\,\text{er}_\text{aAn}} + \text{er}_\text{aO2} m_{S_\text{alk}\,\text{er}_\text{aO2}} + \text{er}_\text{hAn} m_{S_\text{alk}\,\text{er}_\text{hAn}} + \text{er}_\text{hO2} m_{S_\text{alk}\,\text{er}_\text{hO2}} + \text{hy} m_{S_\text{alk}\,\text{hy}} + g_\text{a} m_{S_\text{alk}\,g_\text{a}} + g_\text{hAn} m_{S_\text{alk}\,g_\text{hAn}} + g_\text{hO2} m_{S_\text{alk}\,g_\text{hO2}} + m_{S_\text{alk}\,r_\text{hAn}} r_\text{hAn} + m_{S_\text{alk}\,s_\text{hAn}} s_\text{hAn} + m_{S_\text{alk}\,s_\text{hO2}} s_\text{hO2} \\
\dot{X}_\text{cb} &\coloneqq - \text{hy} \\
\dot{X}_\text{h} &\coloneqq - \text{er}_\text{hAn} - \text{er}_\text{hO2} + g_\text{hAn} + g_\text{hO2} \\
\dot{X}_text{h,s} &\coloneqq g_\text{hAn} m_{X_text{h,s}\,g_\text{hAn}} + g_\text{hO2} m_{X_text{h,s}\,g_\text{hO2}} + m_{X_text{h,s}\,s_\text{hAn}} s_\text{hAn} + m_{X_text{h,s}\,s_\text{hO2}} s_\text{hO2} - r_\text{hAn} - r_\text{hO2} \\
\dot{X}_\text{a} &\coloneqq - \text{er}_\text{aAn} - \text{er}_\text{aO2} + g_\text{a} \\
\label{eq:asm1-ode-state}\end{align}
\begin{align}
\dot{S}_\text{N2} &\coloneqq \text{er}_\text{aAn} m_{S_\text{N2}\,\text{er}_\text{aAn}} + \text{er}_\text{hAn} m_{S_\text{N2}\,\text{er}_\text{hAn}} + g_\text{hAn} m_{S_\text{N2}\,g_\text{hAn}} + m_{S_\text{N2}\,r_\text{hAn}} r_\text{hAn} + m_{S_\text{N2}\,s_\text{hAn}} s_\text{hAn} \\
\dot{S}_\text{nb} &\coloneqq \text{hy} m_{S_\text{nb}\,\text{hy}} \\
\dot{X}_\text{nb} &\coloneqq \text{er}_\text{aAn} m_{X_\text{nb}\,\text{er}_\text{aAn}} + \text{er}_\text{aO2} m_{X_\text{nb}\,\text{er}_\text{aO2}} + \text{er}_\text{hAn} m_{X_\text{nb}\,\text{er}_\text{hAn}} + \text{er}_\text{hO2} m_{X_\text{nb}\,\text{er}_\text{hO2}} \\
\dot{X}_\text{TSS} &\coloneqq \text{er}_\text{aAn} m_{X_\text{TSS}\,\text{er}_\text{aAn}} + \text{er}_\text{aO2} m_{X_\text{TSS}\,\text{er}_\text{aO2}} + \text{er}_\text{hAn} m_{X_\text{TSS}\,\text{er}_\text{hAn}} + \text{er}_\text{hO2} m_{X_\text{TSS}\,\text{er}_\text{hO2}} + \text{hy} m_{X_\text{TSS}\,\text{hy}} + g_\text{a} m_{X_\text{TSS}\,g_\text{a}} + g_\text{hAn} m_{X_\text{TSS}\,g_\text{hAn}} + g_\text{hO2} m_{X_\text{TSS}\,g_\text{hO2}} + m_{X_\text{TSS}\,r_\text{hAn}} r_\text{hAn} + m_{X_\text{TSS}\,r_\text{hO2}} r_\text{hO2} + m_{X_\text{TSS}\,s_\text{hAn}} s_\text{hAn} + m_{X_\text{TSS}\,s_\text{hO2}} s_\text{hO2} \\
\label{eq:asm1-ode-measurement}\end{align}

plt.show()

Total running time of the script: (0 minutes 3.072 seconds)

Estimated memory usage: 88 MB

Gallery generated by Sphinx-Gallery